Trees are a special kind of graphs with some restrictions applied. Trees should have a starting root.
This root node may have links to set of multiple different child nodes. Nodes, which are linked by the same node
called child nodes. If some set of these child nodes are linked by the same parent node, they are called siblings.
Nodes, which don't have children are called leafs.
Parent-child relations in trees are hierarchial. Unlike graphs single child node may not be linked by multiple
parent nodes.
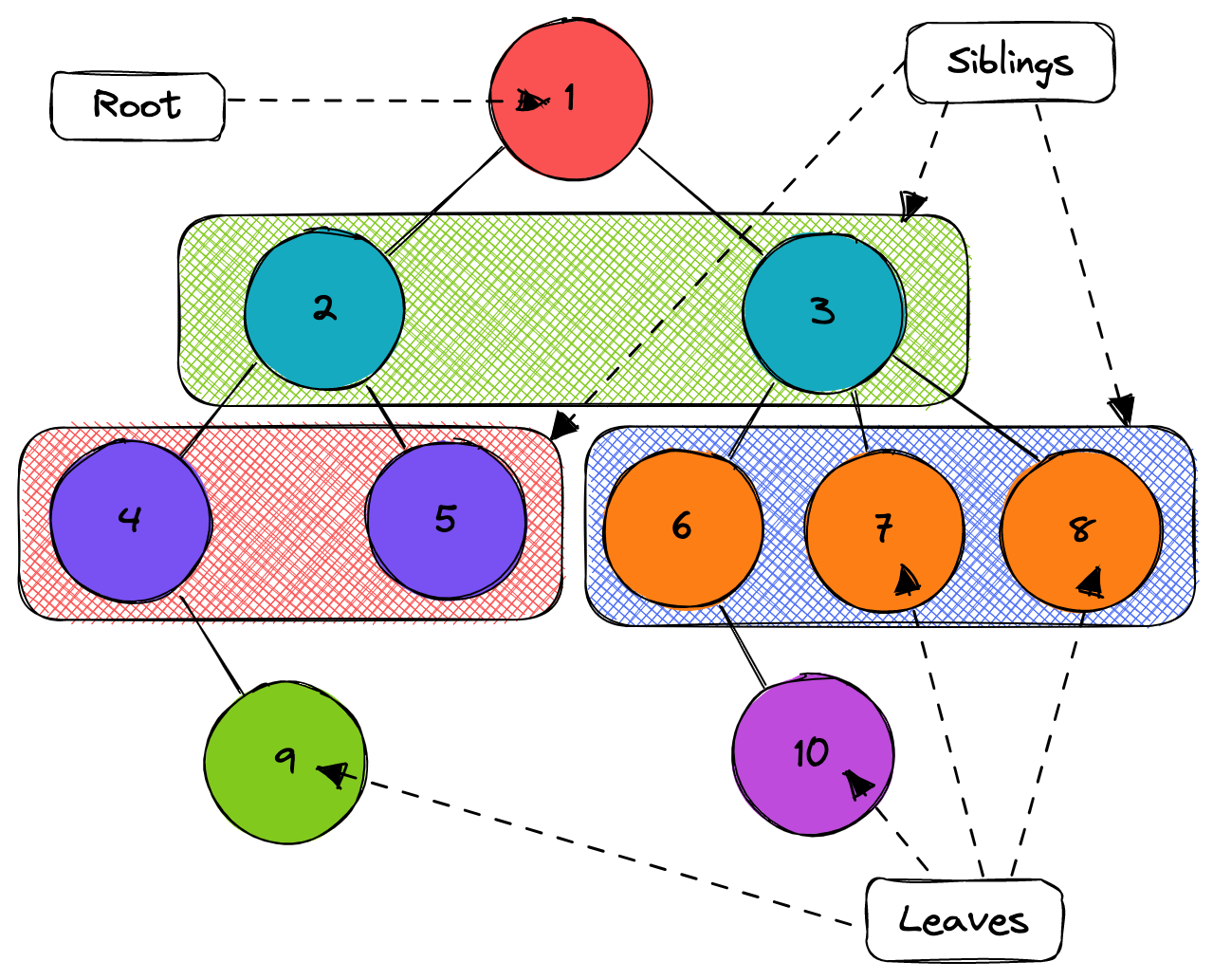
In this example node 1 is a root and parent for nodes 2 and 3, which are siblings, relative to node 1.
In it's turn node 2 is a parent for 4 and 5, which are also siblings. And node 3 is a parent for 6, 7, 8,
which are siblings relative to 3. By analogy node 4 is a parent for 9 and node 6 is a parent for 10. Nodes
7, 8, 9, 10 are leaves, because they don't have children.
When tree has many levels, it is possible to separate it to multiple smaller subtrees with roots in different parent nodes.
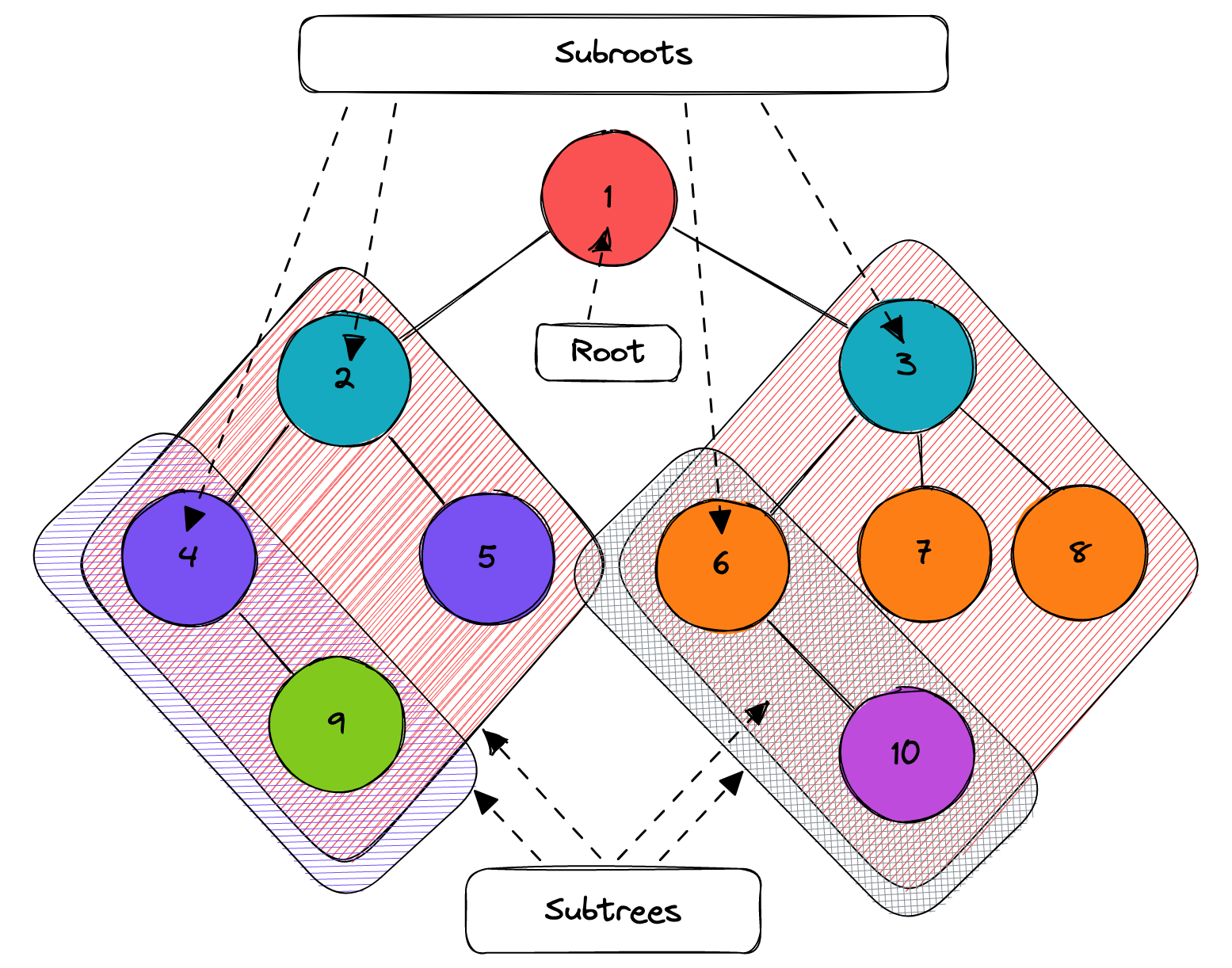
Good to keep this fact in mind when creating algorithms on trees, because this separation is a good fit for recursive algorithms.
Depth And Height
Depth is a parameter of node, which answers the question How far this node is placed from the root. In other words, how
many links we should follow to walk from the root to the required node.
Height shows the longest path from the node to it's most far leaf. Taking height of the root node will give also height
of the whole tree. This will be the longest path to follow in the tree.
Binary Search Tree
Balanced Trees
The tree is balanced if any two sibling subtrees have a difference in their height no more than one level. In other case
tree is considered unbalanced.
Next
https://medium.com/basecs/busying-oneself-with-b-trees-78bbf10522e7 https://medium.com/basecs/painting-nodes-black-with-red-black-trees-60eacb2be9a5 https://medium.com/basecs/the-little-avl-tree-that-could-86a3cae410c7 https://medium.com/basecs/trying-to-understand-tries-3ec6bede0014 https://medium.com/basecs/leaf-it-up-to-binary-trees-11001aaf746d