Graphs

Graph is a data structure, which models set of connections or edges. These connections generally may be not ordered like for array for example. Each node(also may be called vertices) in graph can have many connection to other nodes.

Minimal requirement for graph - to have at least one node.

While many data structures, like trees, tries, linked lists and many others are special cases of graphs and they have some root nodes, in general case graphs may not have any special root element, because there may be many non directional multiple connections between nodes.

Graph Direction

Graphs may be undirected, directed or combined.

When graph is undirected means, that connection between two nodes can lead towards the second node and also backwards. Moreover to be called undirected graph all it's connections have to be undirected. Following example shows equivalent graphs:

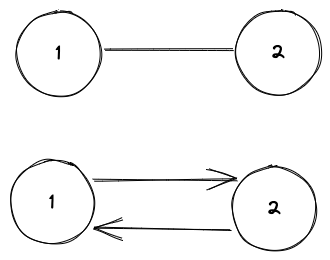
In directed graphs connection always links from one node to another, but opposite does not exist. And by analogy from undirected graphs, to be called directed, graph must have all edges to be directed.

Breadth First Search

This is an algorithm, which allows to get an answer on two question regarding given graph;

• Is there a way from node A to node B
• Which is a shortest way from A to B

Consider following task. We have a graph with nodes of different colors. We need to find shortest way from red node to any orange node.

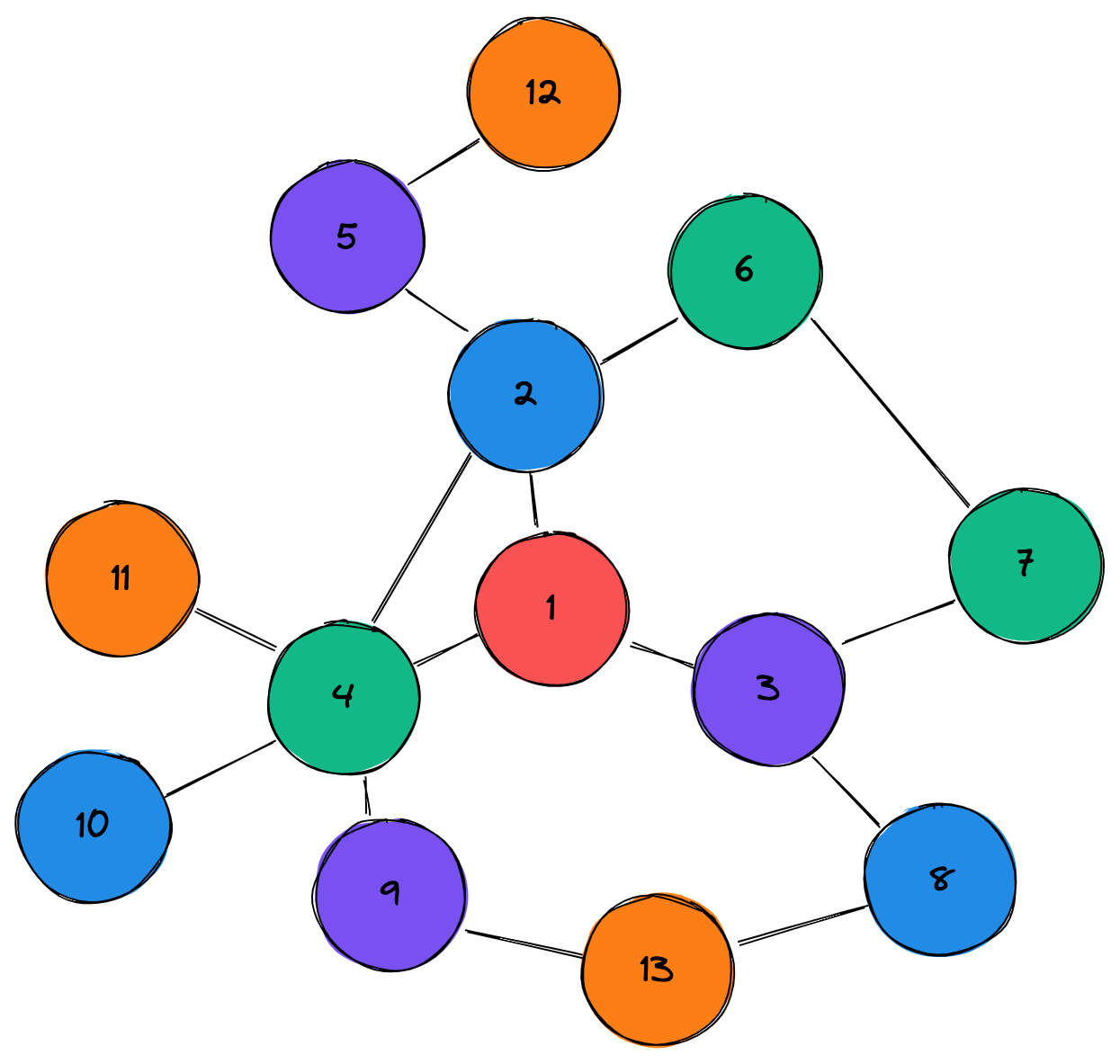
To achieve that, we run simple algorithm. As a first step, we try to find orange node between nodes, which are linked with our initial red node. This is done by simple iteration through list of them. Red node with value 1 linked with nodes indexed 2, 3 and 4. Non of them is orange. Next we try to find orange nodes between relatives of 2, 3 and 4. Those nodes will be 5, 6, 7, 8, 9, 10, 11. Node 11 is orange, which means our search is finished.

As a result we not only found required orange node, but also this node has a shortest path to origin node, where we started our search. Note, that we have other orange nodes 12 and 13, but they have longer path, so these nodes are not the answer.

Other thing that should be highlighted - we have some nodes, which linked by more than one neighbor nodes, e.g. node 4 is linked by nodes 1 and 2. This could be a problem. When we checked relatives of node 1 we check node 4. Then, when there was no answer we go to relatives of node 2 which also points to node 4. But we should not check it for the second time. This means, that we have to track, what nodes have already been checked. Not doing this not only inefficient, but also can lead to cycles. In this case search will not be finished at all.

For example:

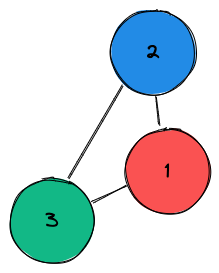
1 points to 2. 2 points to 3 and finally 3 points to 1. Here we are in infinite loop.

Plan

Breadth First Search Dijkstra Algorithm

References

Next

https://medium.com/basecs/finding-the-shortest-path-with-a-little-help-from-dijkstra-613149fbdc8e https://medium.com/basecs/spinning-around-in-cycles-with-directed-acyclic-graphs-a233496d4688 https://medium.com/basecs/deep-dive-through-a-graph-dfs-traversal-8177df5d0f13 https://medium.com/basecs/going-broad-in-a-graph-bfs-traversal-959bd1a09255 https://medium.com/basecs/from-theory-to-practice-representing-graphs-cfd782c5be38